Searching in an sorted and rotated array

This can be done in O(logN) using a slightly modified binary search.

The interesting property of a sorted + rotated array is that when you divide it into two halves, atleast one of the two halves will always be sorted.

Let input array arr = [4,5,6,7,8,9,1,2,3]
number of elements  = 9
mid index = (0+8)/2 = 4

[4,5,6,7,8,9,1,2,3]
         ^
 left   mid  right

as seem right sub-array is not sorted while left sub-array is sorted.

If mid happens to be the point of rotation them both left and right sub-arrays will be sorted.

[6,7,8,9,1,2,3,4,5]
         ^

But in any case one half(sub-array) must be sorted.

We can easily know which half is sorted by comparing start and end element of each half.

Once we find which half is sorted we can see if the key is present in that half - simple comparison with the extremes.

If the key is present in that half we recursively call the function on that half else we recursively call our search on the other half.

We are discarding one half of the array in each call which makes this algorithm O(logN).

/*
 * This Program is used to search for a key in a sorted array which is 
 * rotated. It works fine even if there are duplicates.
 */
public class RotatedArray {
    public static int search(int[] arr, int key, int low, int high) {

        int mid = (low + high) / 2;

        if (arr[mid] == key)
            return mid;
        while (low <= high) {
            // if the left half is sorted.
            if (arr[low] < arr[mid]) {

                // if key is in the left half
                if (arr[low] <= key && key <= arr[mid])
                    // search the left half
                    return search(arr, key, low, mid - 1);
                else
                    // search the right half
                    return search(arr, key, mid + 1, high);
            }

            // if the right half is sorted.
            else if (arr[mid] < arr[low]) {
                // if the key is in the right half.
                if (arr[mid] <= key && arr[high] >= key)
                    return search(arr, key, mid + 1, high);
                else
                    return search(arr, key, low, mid - 1);
            }

            else if (arr[mid] == arr[low]) {

                if (arr[mid] != arr[high])
                    // Then elements in left half must be identical.
                    // Because if not, then it's impossible to have either
                    // arr[mid] < arr[high] or arr[mid] > arr[high]
                    // Then we only need to search the right half.
                    return search(arr, key, mid + 1, high);
                else {
                    // arr[low] = arr[mid] = arr[high], we have to search both
                    // halves.
                    int result = search(arr, key, low, mid - 1);
                    if (result == -1)
                        return search(arr, key, mid + 1, high);
                    else
                        return result;
                }
            }
        }
        return -1;
    }

    public static void main(String args[]) {
        int[] arr = { 2, 2, 2, 2, 2, 3, 1 };
        int high = arr.length;
        int res = search(arr, 3, 0, high - 1);
        System.out.println(res);
    }
}

Reference

Find Minimum in Rotated Sorted Array

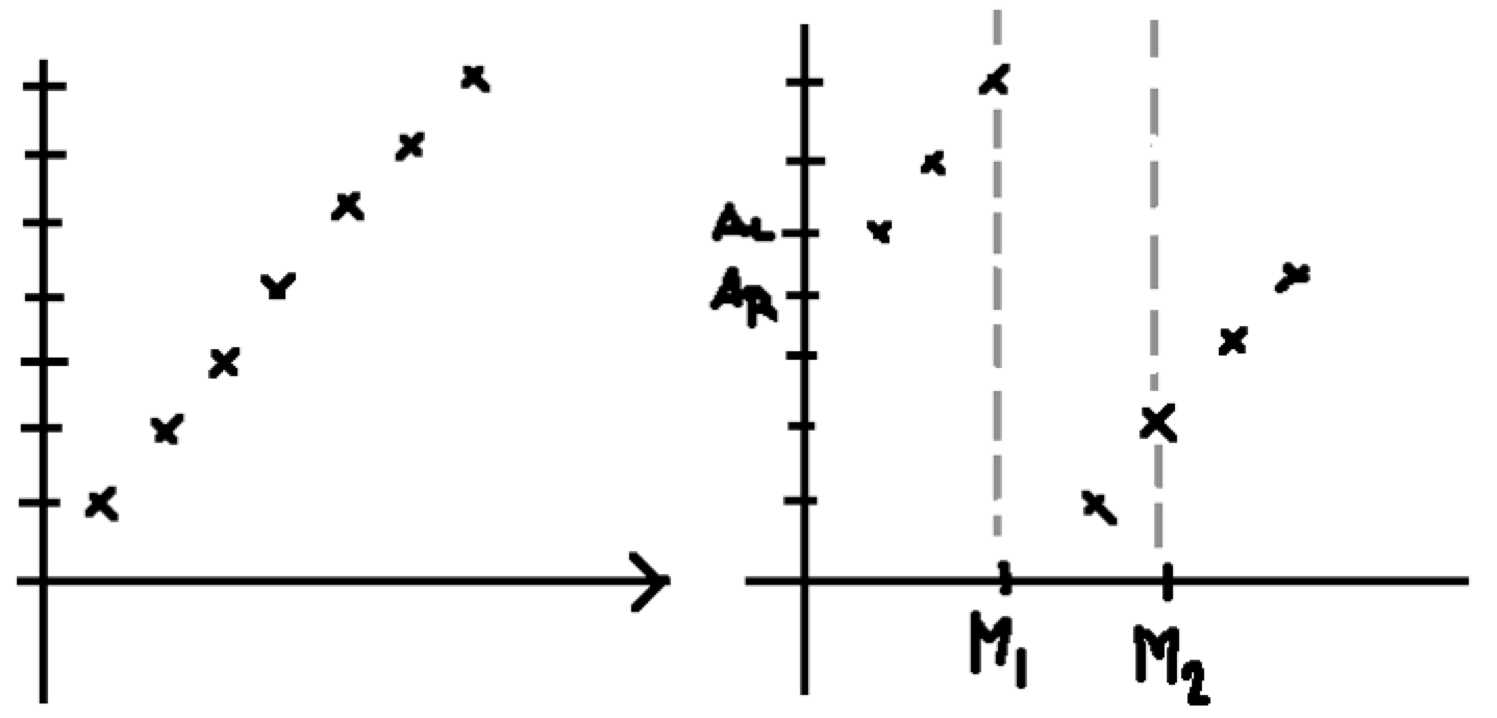
Imagine we have an array [1,2,3,4,5,6,7], See graph 1 which was being rotated 3 steps to the right [5,6,7,1,2,3,4] ,See graph 2. Let’s say we subdivide the array at point k to two subarrays [AL, AL+1, …, Ak], [Ak+1, …, AR].

If the sorted array is not rotated, then AL < AR then we could return AL as the minimum immediately.

Otherwise for a sorted array that was rotated at least one step, AL must always be greater than AR.

Let’s assume we choose M1 as the dividing point. Since AM1 > AR, we know that each element in [AL … AM1] is greater than AR (Remember that AL > AR?). Therefore, the minimum value must locate in [AM1+1 … AR].

On the other hand, let’s assume we choose M2 as the dividing point. Since AM2 ¬≤ AR, we know that each element in [AM2+1 … AR] is greater than AM2. Therefore, the minimum point must locate in [AL … AM2].

As we are discarding half of the elements at each step, the runtime complexity is O(log n).

To understand the correct terminating condition, we look at two elements. Let us choose the lower median as M = (L + R) / 2. Therefore, if there are two elements, it will choose AL as the first element.

There are two cases for two elements:

A = [1,2]
B = [2,1]

For A, 1 < 2 => AM < AR, and therefore it will set R = M => R = 0.

For B, 2 > 1 => AM > AR, and therefore it will set L = M + 1 => L = 1.

Therefore, it is clear that when L == R, we have found the minimum element.

public int findMin(int[] num) {
        int n = num.length;
        int end = n-1;
        int start = 0;
        if(num==null||n==0) return 0;
        if(n==1) return num[0];
        while(start<end)
        {
            int mid = (start+end)/2;
            if(mid>0 && num[mid-1]>num[mid]) return num[mid];
            if(num[mid]>num[end]) start = mid+1;
            else end = mid-1;
        }
     return num[start];   
    }

Refrence :
https://oj.leetcode.com/

Memoized Fibonacci

The Fibonacci Sequence is the series of numbers:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

The next number is found by adding up the two numbers before it.

The 2 is found by adding the two numbers before it (1+1) Similarly, the 3 is found by adding the two numbers before it (1+2), And the 5 is (2+3), and so on!

The Rule is  F(n) =  F(n-1) +  F(n-2)

A recurive function for calculating nth Fibo can be given by the following code.

  fib(int n)
    {
        if(n==0) return 0L;
        if(n==1) return 1L;
        return fib(n-1)+fib(n-2);

    }

The recursion tree is given below, here we can see that there are lot of values which are computed multiple times. Thus this approach has multiple duplicate calculations. We can remember previously computed values and use them instead of recomputing them.

                         F(n)
                        /    \
                    F(n-1)   F(n-2)
                    /   \     /      \
                F(n-2) F(n-3) F(n-3)  F(n-4)
               /    \
             F(n-3) F(n-4)

One approach to remmeber the values is by storing them in HashMap and use them for later use because the lookup is O(1).

import java.util.*;
public class Fibo{
    public static Long fibWithMemo(int n)
    {
        HashMap<Integer,Long> data = new HashMap<Integer,Long>();
        Long prev =  0L;
        Long cur = 1L;
        data.put(0,prev);
        data.put(1,cur);
        for(int i=2;i<=n;i++)
            data.put(i,data.get(i-1)+data.get(i-2));
    return data.get(n);
    }

    public static Long fib(int n)
    {
        if(n==0) return 0L;
        if(n==1) return 1L;
        return fib(n-1)+fib(n-2);

    }

    public static void main(String args[])
    {
        long start,elapsedTime;
        start = System.nanoTime();
        System.out.println(fibWithMemo(40));
        elapsedTime = System.nanoTime()-start;
        System.out.println("Time for fibWithMemo "+elapsedTime);
        start = System.nanoTime();
        System.out.println(fib(40));
        elapsedTime = System.nanoTime()-start;
        System.out.println("Time for fib "+elapsedTime);

    }

}

The ouput of the above program is :

rohan@rohan-Inspiron-1545:~/Algorithms$ java Fibo
102334155
Time for fibWithMemo 3462173
102334155
Time for fib 2981581808

Recursion

Recursion is powerful tool to solve many problems with simple and elegant code, but it is often tricky to imagine how the function calls are being made. I will try to take a problem and explain the flow of recursive calls.

Given a positive integer, return its corresponding column title as appear in an Excel sheet.

For example: 1 -> A 2 -> B 3 -> C ... 26 -> Z 27 -> AA 28 -> AB

This problem can be solved using a recursive function and it turns out to be a single line of code.

public class ExcelTitle {
    public static String convertToTitle(int n) {
        return n == 0 ? "" : convertToTitle(--n / 26) + (char)('A' + (n % 26));

    }

    public static void main(String args[])
    {
        System.out.println(convertToTitle(27));


    }
}

The explanation is shown in the screenshot below:

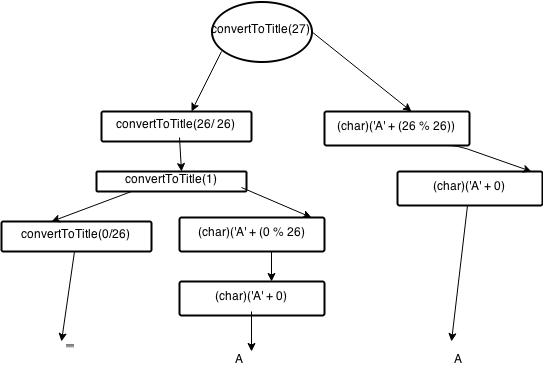
The output of the call convertToTitle(27) is AA.

Python Notes

This post conatins Python programming notes, from the Python tutorial that is offered by Google

Basics

• sys.argv[0] ---- program name itself
• arguments and variables similar no types

def Hello(name):
    a = 'hello'

• print seperate by , then space is includes automatically
• print 'Hello',name,a ===> Hello rohan!!! 10
• print'Hello'+name+str(a) ⇒ Hellorohan!!!10
• string not empty, num is not 0 -- > true

How python works

• does everything at last possible second
• in the moment it checks at every line
• strings are immutable (returns new string)
• a.find() - returns first occurance
• a.lower()
• place holder %
• 'Hi %s I have %d donuts' % (‘Alice’,29)
• These are not python strings and not unicode strings these are just series of bytes.

Strings slice

>>> a = 'Hello'
>>> a
'Hello'
>>> a[1:3]
'el'
>>> a[1:2]
'e'
>>> a[1:5]
'ello'
>>> a[1:]
'ello'
>>> a[:5]
'Hello'
>>> a[:]
'Hello'

Negatives

>>> a = 'Hello'
>>> a[-1]
'o'
>>> a[-3:]
'llo'
>>> a[-3:-1]
'll'

Lists

• Same syntax across all
• a = [1,2,3,’a’]
• len(a) to find length
• b = a (does not create a copy both point to same)
• lists are 'mutable'
• python has garbage collector {need to make copies is not much}
• a ==b does the same returns true
• slices works fine with lists as well
• There is built in for each for var in list: print var
  
• Check if value in a list {works for lot of DS - in hash table does }
• value in list
• Built in for lists
• append - does not return new list returns None
• a = [1,2,3]
• a.append(4)
• a = a.append(4) # error NO NO
• a.pop(0) pops of element and returns it
• delete a from local scope
• del a {complete list}
• del a[1] {delete a element}
• The range(n) function yields the numbers 0, 1, ...
• for i in range(100) print i

Sorting

• sorting of lists - don't use .sort()
• sorted - makes a new list and sorts.
• comparison depends on the type of elements compared.{strings,ints,char}

Custom sorting

• old way 2 argument comparator method. python has new way
• sort by length

>>> sorted(a,key=len)
['d', 'a', 'dc', 'aa', 'ccc']
>>> def last(s): return s[-1]

>>> sorted(a,key=last)
['a', 'aa', 'ccc', 'dc', 'd']
split, join
>>> ':'.join(a)
'z:d:dc:a:aa'
>>> '\n'.join(a)
'z\nd\ndc\na\naa'
>>> ':'.join(a)
'z:d:dc:a:aa'
>>> b = ':'.join(a)
>>> b.split(':')
['z', 'd', 'dc', 'a', 'aa']

• Don’t modify list while iterating a list (even java has same constraint)

Tuple

• Fixed size
• immutable
• tup = (1,2,3)
• (x,y,z) coordinates; (url,score) {taking fixed number of strings and pass together)

>>> a = (1,3,3)
>>> a
(1, 3, 3)
>>> len(a)
3
>>> a[0]
1
>>> a[0]=2
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: 'tuple' object does not support item assignment
Sort by one thing and then sort by other 
Write key function that returns a tuple
>>> a = [(1,"b"),(2,"a"),(1,"a")]
>>> a
[(1, 'b'), (2, 'a'), (1, 'a')]
>>> sorted(a)
[(1, 'a'), (1, 'b'), (2, 'a')]
Parallel assignment 
>>> (x,y) = (1,2)

HashTable , /Dictionary

• {}
• key,value bindings
• constant time retrieval

>>> d ={}
>>> d['a'] = 'alpha'
>>> d['a']
'alpha'
>>> d['B']
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
KeyError: 'B'

get(),keys(),items()

d.get()
>>> d.get('a')
'alpha'
>>> d.get('f')
how to find if something is in dict
‘a’ in d
True
.keys()

>>> d.keys()
['a']
>>> d['b'] = 'beta'
>>> d.keys()
['a', 'b']
values()
>>> d.values()
['alpha', 'beta']

looping

>>> for k in sorted(d.keys()): print 'key:',k,'->',d[k]
... 
key: a -> alpha
key: b -> beta
d.items()
    >>> d.items()
[('a', 'alpha'), ('b', 'beta')]
>>> for tuple in d.items(): print tuple
... 
('a', 'alpha')
('b', 'beta')

Files

• creating cat python
• f = open(filename,'r')
• diff modes - 'r','w''rU' text = f.read() lines = f.readlines() f.open(fname,”w”) f.write(text) {be careful we can zero out file}

Regular Expression

• import re
• returns a match object
• match = re.search(pattern,text)
• match = re.search(‘iig’,’its a piiiiiiiig’)
• if match:
• . dot any character except new line --\w word character --\d digit --\s space
• left to right once it finds solution it is done
• if looking for period char >>> Find('a\.','its a. piiiiiiiig') a.
• raw string
  • do not do any special processing with backslashes
• uses for writing regex

\S non whitespace
\s whitespace
\d digit 0-9
\w word character a-z A-Z 0-9

Email example

>>> m = re.search(r'([\w.]+)@([\w.]+)','egrreg gjkenrkj@snfjkv.com erngjk @ ')
>>> m
<_sre.SRE_Match object at 0xb7467800>
>>> m.group()
'gjkenrkj@snfjkv.com'
>>> m.group(1)
'gjkenrkj'
>>> m.group(2)
'snfjkv.com'
>>> m = re.search(r'([\w.]+)@([\w.]+)','egrreg gjken.rkj@snfjkv.com erngjk @ ')
>>> m
<_sre.SRE_Match object at 0xb7467140>
>>> m.group(1)
'gjken.rkj'
>>> m.group(2)
'snfjkv.com'
findall()
    >>re.findall(r'[\w.]+@[\w.]+','egrreg@fmail.com gjken.rkj@snfjkv.com erngjk @ ')
['egrreg@fmail.com', 'gjken.rkj@snfjkv.com']

 re.findall(r'([\w.]+)@([\w.]+)','egrreg@fmail.com gjken.rkj@snfjkv.com erngjk @ ')
[('egrreg', 'fmail.com'), ('gjken.rkj', 'snfjkv.com')]

Flags

• DOTALL also matches newline aswell
• how to use constants >>> m = re.search(r'rohan','ROHAN',re.IGNORECASE) >>> m <_sre.SRE_Match object at 0xb726b3d8> >>> m.group() 'ROHAN'

Modules

• os module
• platform independent systime
• listdir(path) ----> list of strings
  1. import os
os.path.exists(‘/tmp/foo’)
  2. import shutil
shutil.copy(source, dest) ---- >file copying
  3. import commands
     launch a external process and wait for it to finish
     commands.getstatusoutput(cmd)
     returns a tuple of length 2 (status,output) 1st int exit code 2nd is all output std output and std error
• zip -j name all absolute paths

Exceptions

def cat(filename):
  try:
    f = open(filename, 'rU') #U ignare dos line ending unix
    print '-----',filename
    text = f.read() #having just 1 string
    print text
    f.close()
  except IOError:
    print 'No File',filename 
def main():
  args = sys.argv[1:]
  for arg in args:
    cat(arg)

Modularity

• just .py file namespace
• when we load a python file it runs (do not wrie print outside)
  >>> import babynames Hi There !!! >>> dir(babynames) ['__builtins__', '__doc__', '__file__', '__name__', '__package__', 'extract_names', 'main', 're', 'sys'] >>help(babynames.extract_names)

urllib

• Takes url and makes it to look like a file
• import urllib
• Takes a url and tries to look like a file
• uf = urllib.urlopen(‘http://google.com’)
• uf.read()
• has lots of features , set cookies >>> urllib.urlretrieve('http://google.com/intl/en_ALL/images/logo.gif','blah.gif') ('blah.gif', <httplib.HTTPMessage instance at 0xb6fa870c>)